任务描述:
1>制作一个手机端的手绘板
2>要求能有毛笔的笔锋
3>画线能有轻重感
4>能重播手写过程
5>能提交保存
现在,我们来着重解决第三个问题,画线能有轻重感,手指一接触触摸屏,js就会在相应的位置画上一个填充圆,然后缓慢的移动手指,会发现线条渐渐变粗,也就实现了重笔画的手写过程,手指仍然不要松开,现在我们突然加速,会发现,很突兀的一下,线条就变细了,经过多方的想法,最终我想到了一个办法。
两圆之间的公切线会让线条平滑。
但是两圆公切线怎么计算呢?
下面是初始计算公式:
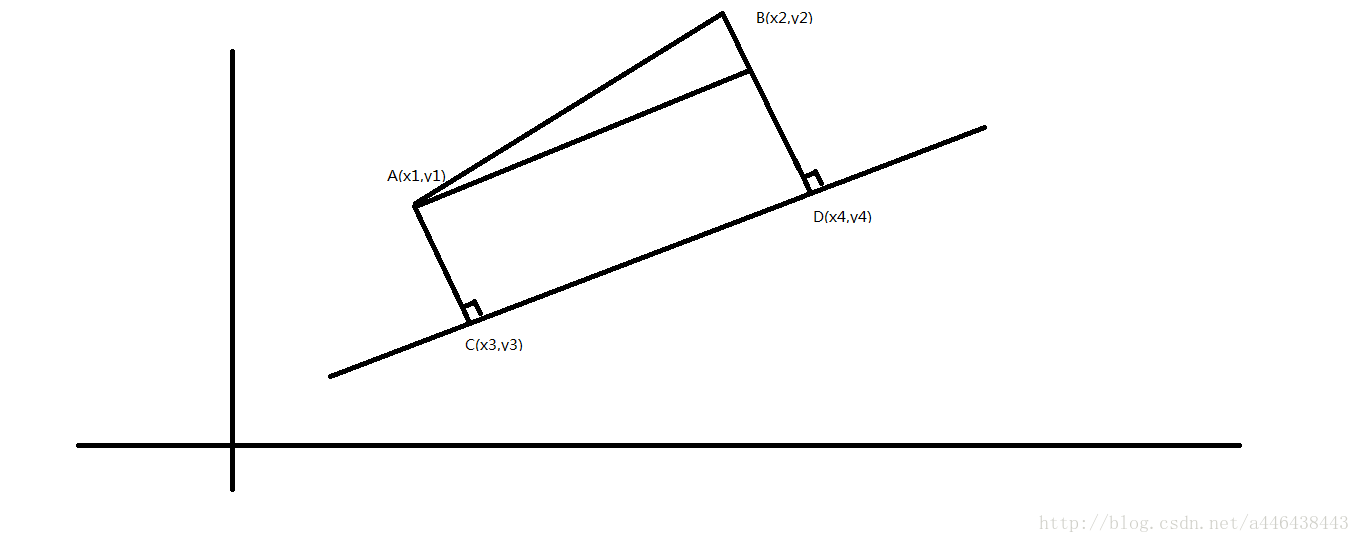
如图:
A是圆1的圆心,AC是圆1的半径
B是圆2的圆心,BD是圆2的半径
C是圆1关于CD的切点,D是圆2关于CD的切点
那么有点到点的距离公式可以获得下面几个方程:
①(x1-x3)^2+(y1-y3)^2=AC^2
②(x2-x4)^2+(y2-y4)^2=BD^2
③(x1-x2)^2+(y1-y2)^2=AB^2
④(x2-x3)^2+(y2-y3)^2=BC^2
⑤(x1-x4)^2+(y1-y4)^2=AD^2
其中AC和BD已知,AB可以由两点之间的距离公式②算出。
过点A做BD的垂线,交点为E(x5,y5)
∵BE=BD-DE
DE=AC
∴BD=BD-AC
根据勾股定理可以得到:
⑥AE^2=AB^2-BE^2
公式①和④推导出如下公式:
y3(4(y1-y2)^2-(4x2-x1)^2)-2y3((2(y1-y2)(r2^2-r1^2+ED^2-(x2+x1)^2+(y1-y2)^2))-y1(4x2+x1)^2)+(r2^2-r1^2+ED^2-(x2+x1)^2+(y1^2-y2^2))^2-y1^2(4x2+x1)^2=0
可以得到一元二次方程式中的a,b,c分别为如下
假设y1=startY,x1=startX,x2=endX,y2=endY,r1=startW,r2=endW;
则可以得到如下表达式
$a=4*sqr($startY-$endY)-sqr($startX-4*$endX); //sqr函数是求平方函数,自己动手写的。
$b=2*(2*($startY-$endY)*(sqr($endW)-sqr($startW)-sqr($endX+$startX)+$ED+sqr($startY-$endY))-$startY*sqr(4*$endX+$startX));
$c=sqr(sqr($endW)-sqr($startW)+$ED-sqr($endX+$startX)+sqr($startY)-sqr($endY))-sqr($startY)*sqr(4*$endX+$startX);
求解:
最后得到如下表达式:
<span style="white-space:pre"> </span>$x1=(-$b+ sqrt(sqr($b)-4*$b*$c))/(2*$a);
$x2=(-$b- sqrt(sqr($b)-4*$b*$c))/(2*$a);
$y1=sqrt(sqr($startW)-sqr($x1-$startX))+$startY;
$y2=sqrt(sqr($startW)-sqr($x2-$startX))+$startY;经过运算,此算法错误。详情请参照下篇文章。
